Venn Diagram is one of the easiest ways to visualize the Bayes Rule. For that, I take a classical example of computing probability of cancer given the test result is positive.

Anatomy of a Test

  • 1% of women have breast cancer (and therefore 99% do not).
  • 80% of mammograms detect breast cancer when it is there (and therefore 20% miss it).
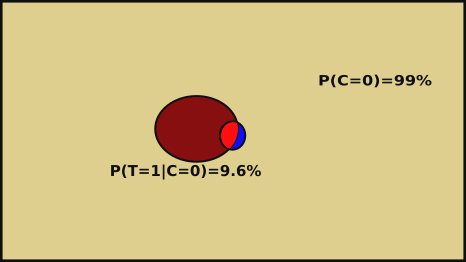
  • 9.6% of mammograms detect breast cancer when it’s not there (and therefore 90.4% correctly return a negative result).

Now suppose a person get a positive test result. What are the chances the person has cancer?

80%? 99%? 1%?

It looks like the right hand side of Bayes Formula. COOL!!

Venn Diagram of cancer test information

Bayes rule 1

Area representing women having cancer (C=1) : Bayes_cancer

Probability of breast cancer P(C=1) = 1%

Probability of not having cancer P(C=0) = (100 - 1)% = 99 %

cancer_identified

Area representing positive result (T) (saying the woman has cancer) P(T=1): positive_test

Hence, P(C=1|T=1) = cancer_given_test_true

Visually problem is solved

Using the areas to compute the probability.

80% of women having cancer are identified by test P(T=1|C=1) = 80% = test_true_given_cancer

$P(T \cap C)$ = 80% of 1% = 0.8 * 0.01 = 0.008 = cancer_identified

= total_test_true

= 0.09504 + 0.008 = 0.10304

Probability of cancer given test is positive $P(C=1|T= 1)$ = cancer_given_test_true = 0.008/ 0.10304

= 0.0776 = 7.76%

Using Bayes Formula

cancer_given_test_true

References: